作者:Vamei 出处:http://www.cnblogs.com/vamei 欢迎转载,也请保留这段声明。谢谢!
排序算法(Sorting Algorithm)是计算机算法的一个组成部分。排序算法是将一个序列按照大小顺序重新排列。排序是古老但依然富有挑战的问题。Donald Knuth的经典之作《计算机程序设计艺术》(The Art of Computer Programming)的第三卷就专门用于讨论排序和查找。从无序到有序,从统计物理的角度看,就是减小了系统的熵值,增加了系统的有序度。有序这一特征是关于系统的非常有用的先验知识。因此,排序算法可以作为其他快速算法的基础,比如二分法就是基于有序序列的查找算法。直到今天,排序算法依然是计算机科学积极探索的一个方向。
我在这里列出一些最常见的排序方法,并使用C语言实现。序列表示为一个数组a,数组有n个元素。a[i]为数组中的一个元素,i为元素在数组中的位置(下标)。根据C的规定,数组下标从0开始。假设数组从左向右排列,下标为0的元素位于数组的最左边。
序列将最终排列成从小到大的顺序。下面函数中的参数ac是数组中元素的数目,也就是n。
(C语言的数组名都转成指针,传递给函数,所以需要传递数组中元素的数目ac给函数,详细见"Expert C Programming: Deep C Secrets"一书)
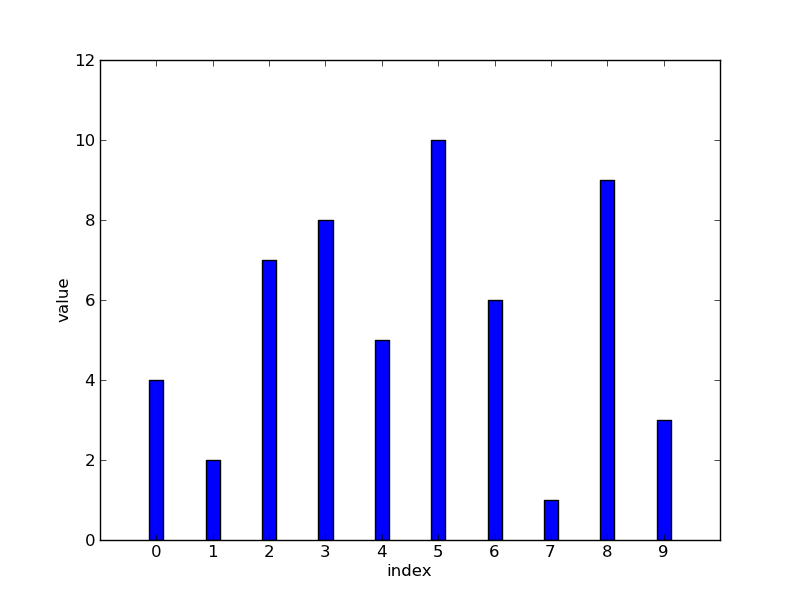
起始数列 (unsorted)
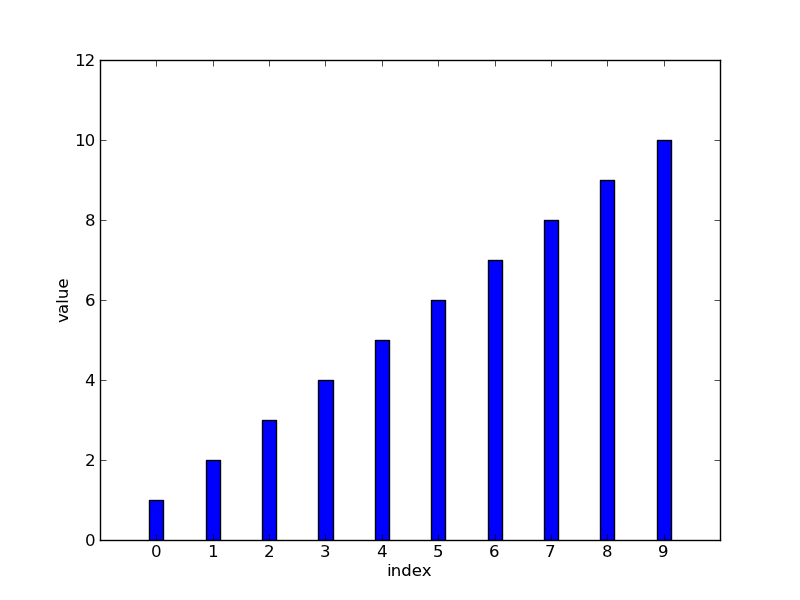
有序数列 (sorted)
下面的链接中,有相关算法的动画图例,强烈推荐同时阅读。
冒泡排序 (Bubble Sort)
如果序列是从小到大排列好的,那么任意两个相邻元素,都应该满足a[i-1] <= a[i]的关系。在冒泡排序时,我们从右向左遍历数组,比较相邻的两个元素。如果两个元素的顺序是错的,那么就交换这两个元素。如果两个元素的顺序是正确的,则不做交换。经过一次遍历,我们可以保证最小的元素(泡泡)处于最左边的位置。
经过一次遍历,冒泡排序并不能保证所有的元素已经按照从小到大的排列好。因此,我们需要重新从右向左遍历数组元素,并进行冒泡排序。这一次遍历,我们不用考虑最左端的元素。然后继续进行最多为n-1次的遍历。
如果某次遍历过程中,元素都没有发生交换,那么说明数组已经排序好,可以中止停止排序。最坏的情况是在起始数组中,最大的元素位于最左边,那么冒泡算法必须经过n-1次遍历才能将数组排列好,而不能提前完成排序。
/*By Vamei*/ /*swap the neighbors if out of order*/void bubble_sort(int a[], int ac){ /*use swap*/ int i,j; int sign; for (j = 0; j < ac-1; j++) { sign = 0; for(i = ac-1; i > j; i--) { if(a[i-1] > a[i]) { sign = 1; swap(a+i, a+i-1); } } if (sign == 0) break; }}
插入排序 (Insertion Sort)
假设在新生报到的时候,我们将新生按照身高排好队(也就是排序)。如果这时有一名学生加入,我们将该名学生加入到队尾。如果这名学生比前面的学生低,那么就让该学生和前面的学生交换位置。这名学生最终会换到应在的位置。这就是插入排序的基本原理。
对于起始数组来说,我们认为最初,有一名学生,也就是最左边的元素(i=0),构成一个有序的队伍。
随后有第二个学生(i=1)加入队伍,第二名学生交换到应在的位置;随后第三个学生加入队伍,第三名学生交换到应在的位置…… 当n个学生都加入队伍时,我们的排序就完成了。
/*By Vamei*//*insert the next element into the sorted part*/void insert_sort(int a[], int ac){ /*use swap*/ int i,j; for (j=1; j < ac; j++) { i = j-1; while((i>=0) && (a[i+1] < a[i])) { swap(a+i+1, a+i); i--; } }}
选择排序 (Selection Sort)
排序的最终结果:任何一个元素都不大于位于它右边的元素 (a[i] <= a[j], if i <= j)。所以,在有序序列中,最小的元素排在最左的位置,第二小的元素排在i=1的位置…… 最大的元素排在最后。
选择排序是先找到起始数组中最小的元素,将它交换到i=0;然后寻找剩下元素中最小的元素,将它交换到i=1的位置…… 直到找到第二大的元素,将它交换到n-2的位置。这时,整个数组的排序完成。
/*By Vamei*//*find the smallest of the rest, then append to the sorted part*/void select_sort(int a[], int ac) { /*use swap*/ int i,j; int min_idx; for (j = 0; j < ac-1; j++) { min_idx = j; for (i = j+1; i < ac; i++) { if (a[i] < a[min_idx]) { min_idx = i; } } swap(a+j, a+min_idx); } }
希尔排序 (Shell Sort)
我们在冒泡排序中提到,最坏的情况发生在大的元素位于数组的起始。这些位于数组起始的大元素需要多次遍历,才能交换到队尾。这样的元素被称为乌龟(turtle)。
乌龟元素的原因在于,冒泡排序总是相邻的两个元素比较并交换。所以每次从右向左遍历,大元素只能向右移动一位。(小的元素位于队尾,被称为兔子(rabbit)元素,它们可以很快的交换到队首。)
希尔排序是以更大的间隔来比较和交换元素,这样,大的元素在交换的时候,可以向右移动不止一个位置,从而更快的移动乌龟元素。比如,可以将数组分为4个子数组(i=4k, i=4k+1, i=4k+2, i=4k+3),对每个子数组进行冒泡排序。比如子数组i=0,4,8,12...。此时,每次交换的间隔为4。
完成对四个子数组的排序后,数组的顺序并不一定能排列好。希尔排序会不断减小间隔,重新形成子数组,并对子数组冒泡排序…… 当间隔减小为1时,就相当于对整个数组进行了一次冒泡排序。随后,数组的顺序就排列好了。
希尔排序不止可以配合冒泡排序,还可以配合其他的排序方法完成。
/*By Vamei*//*quickly sort the turtles at the tail of the array*/void shell_sort(int a[], int ac){ int step; int i,j; int nsub; int *sub; /* initialize step */ step = 1; while(step < ac) step = 3*step + 1; /* when step becomes 1, it's equivalent to the bubble sort*/ while(step > 1) { /* step will go down to 1 at most */ step = step/3 + 1; for(i=0; i Shell Sorting依赖于间隔(step)的选取。一个常见的选择是将本次间隔设置为上次间隔的1/1.3。见参考书籍。
归并排序 (Merge Sort)
如果我们要将一副扑克按照数字大小排序。此前已经有两个人分别将其中的一半排好顺序。那么我们可以将这两堆扑克向上放好,假设小的牌在上面。此时,我们将看到牌堆中最上的两张牌。
我们取两张牌中小的那张取出放在手中。两个牌堆中又是两张牌暴露在最上面,继续取小的那张放在手中…… 直到所有的牌都放入手中,那么整副牌就排好顺序了。这就是归并排序。
下面的实现中,使用递归:
/*By Vamei*//*recursively merge two sorted arrays*/void merge_sort(int *a, int ac){ int i, j, k; int ac1, ac2; int *ah1, *ah2; int *container; /*base case*/ if (ac <= 1) return; /*split the array into two*/ ac1 = ac/2; ac2 = ac - ac1; ah1 = a + 0; ah2 = a + ac1; /*recursion*/ merge_sort(ah1, ac1); merge_sort(ah2, ac2); /*merge*/ i = 0; j = 0; k = 0; container = (int *) malloc(sizeof(int)*ac); while(i
快速排序 (Quick Sort)
我们依然考虑按照身高给学生排序。在快速排序中,我们随便挑出一个学生,以该学生的身高为参考(pivot)。然后让比该学生低的站在该学生的右边,剩下的站在该学生的左边。
很明显,所有的学生被分成了两组。该学生右边的学生的身高都大于该学生左边的学生的身高。
我们继续,在低身高学生组随便挑出一个学生,将低身高组的学生分为两组(很低和不那么低)。同样,将高学生组也分为两组(不那么高和很高)。
如此继续细分,直到分组中只有一个学生。当所有的分组中都只有一个学生时,则排序完成。
在下面的实现中,使用递归:
/*By Vamei*//*select pivot, put elements (<= pivot) to the left*/void quick_sort(int a[], int ac){ /*use swap*/ /* pivot is a position, all the elements before pivot is smaller or equal to pvalue */ int pivot; /* the position of the element to be tested against pivot */ int sample; /* select a pvalue. Median is supposed to be a good choice, but that will itself take time. here, the pvalue is selected in a very simple wayi: a[ac/2] */ /* store pvalue at a[0] */ swap(a+0, a+ac/2); pivot = 1; /* test each element */ for (sample=1; sample 理想的pivot是采用分组元素中的中位数。然而寻找中位数的算法需要另行实现。也可以随机选取元素作为pivot,随机选取也需要另行实现。为了简便,我每次都采用中间位置的元素作为pivot。
堆排序 (Heap Sort)
堆(heap)是常见的数据结构。它是一个有优先级的队列。最常见的堆的实现是一个有限定操作的Complete Binary Tree。这个Complete Binary Tree保持堆的特性,也就是父节点(parent)大于子节点(children)。因此,堆的根节点是所有堆元素中最小的。堆定义有插入节点和删除根节点操作,这两个操作都保持堆的特性。
我们可以将无序数组构成一个堆,然后不断取出根节点,最终构成一个有序数组。
堆的更详细描述请阅读参考书目。
下面是堆的数据结构,以及插入节点和删除根节点操作。你可以很方便的构建堆,并取出根节点,构成有序数组。
/* By Vamei Use an big array to implement heap DECLARE: int heap[MAXSIZE] in calling function heap[0] : total nodes in the heap for a node i, its children are i*2 and i*2+1 (if exists) its parent is i/2 */void insert(int new, int heap[]) { int childIdx, parentIdx; heap[0] = heap[0] + 1; heap[heap[0]] = new; /* recover heap property */ percolate_up(heap);}static void percolate_up(int heap[]) { int lightIdx, parentIdx; lightIdx = heap[0]; parentIdx = lightIdx/2; /* lightIdx is root? && swap? */ while((parentIdx > 0) && (heap[lightIdx] < heap[parentIdx])) { /* swap */ swap(heap + lightIdx, heap + parentIdx); lightIdx = parentIdx; parentIdx = lightIdx/2; }}int delete_min(int heap[]) { int min; if (heap[0] < 1) { /* delete element from an empty heap */ printf("Error: delete_min from an empty heap."); exit(1); } /* delete root move the last leaf to the root */ min = heap[1]; swap(heap + 1, heap + heap[0]); heap[0] -= 1; /* recover heap property */ percolate_down(heap); return min;}static void percolate_down(int heap[]) { int heavyIdx; int childIdx1, childIdx2, minIdx; int sign; /* state variable, 1: swap; 0: no swap */ heavyIdx = 1; do { sign = 0; childIdx1 = heavyIdx*2; childIdx2 = childIdx1 + 1; if (childIdx1 > heap[0]) { /* both children are null */ break; } else if (childIdx2 > heap[0]) { /* right children is null */ minIdx = childIdx1; } else { minIdx = (heap[childIdx1] < heap[childIdx2]) ? childIdx1 : childIdx2; } if (heap[heavyIdx] > heap[minIdx]) { /* swap with child */ swap(heap + heavyIdx, heap + minIdx); heavyIdx = minIdx; sign = 1; } } while(sign == 1);}
总结
除了上面的算法,还有诸如Bucket Sorting, Radix Sorting涉及。我会在未来实现了相关算法之后,补充到这篇文章中。相关算法的时间复杂度分析可以参考书目中找到。我自己也做了粗糙的分析。如果博客园能支持数学公式的显示,我就把自己的分析过程贴出来,用于引玉。
上面的各个代码是我自己写的,只进行了很简单的测试。如果有错漏,先谢谢你的指正。
最后,上文中用到的交换函数为:
/* By Vamei *//* exchange the values pointed by pa and pb*/void swap(int *pa, int *pb){ int tmp; tmp = *pa; *pa = *pb; *pb = tmp;}
参考书目
Data Structures and Algorithm Analysis in C, Mark Allen Weiss
Algorithms in C, Robert Sedgewick